Електричне
поле та його характеристики
 |
| Прояв електричного поля. |
Електричні
заряди не діють безпосередньо один на одний. Кожне заряджене тіло створює в
навколишньому просторі електричне поле. Це поле зумовлює силову
дію на інші заряджені тіла.
Головна
властивість електричного поля – дія на електричні заряди з деякою силою. Отже,
взаємодія заряджених тіл здійснюється завдяки електричному полю, яке оточує
заряджені тіла.
Електричне
поле, яке оточує заряджене тіло, можна досліджувати за допомогою так званого пробного заряду – невеликого по величині точкового заряду, який не
вносить помітного перерозподілу досліджуваних електричних полів.
Для
кількісного визначення електричного поля вводять силову характеристику
електричного поля - напруженість електричного поля.
Напруженістю
електричного поля називають фізичну величину, яка дорівнює відношенню сили, з
якою поле діє на позитивний пробний заряд, поміщений в дану точку простору, до
величини цього заряду:
E =
F/q
Напруженість
електричного поля – векторна фізична величина. Напрям вектора E співпадає в
кожній точці простору з напрямом сили, яка діє на додатний пробний заряд.
Електричне
поле нерухомих і не змінних з часом
зарядів називають електростатичним.
Якщо
за допомогою пробного заряду досліджують електричне поле, яке створене кількома
зарядженими тілами, то результуюча сила буде рівною геометричній сумі сил, які
діють на пробний заряд з боку кожного зарядженого тіла зокрема. Отже,
напруженість електричного поля, яке створене системою зарядів в деякій точці
простору, дорівнює векторній сумі напруженостей електричних полів, створених в
тій же точці кожним зарядом зокрема:
E = E1 + E2 + E3 + …
Ця
властивість електричного поля свідчить, що для електричного поля справджується
принцип суперпозиції.
За
законом Кулона, напруженість електростатичного поля, яке створене точковим
зарядом Q на віддалі r от нього, дорівнює по модулю:
E = kQ/r2
Це
поле називають кулонівським.
В кулонівському полі напрям вектора E залежить від
знаку заряду Q:
- якщо Q > 0, то вектор E напрямлений вздовж радіуса від заряда,
- якщо Q < 0, то вектор E напрямлений вздовж радіуса в бік заряда.
Електростатичне
поле зображають за допомогою силових ліній.
Ці
лінії проводять так, щоб напрям вектора Е в кожній точці співпадав з напрямом
дотичної до силових ліній (мал. 1). При зображенні електричного поля за
допомогою силових ліній, їх густина має бути пропорційною модулю вектора
напруженості електричного поля.
Силові
лінії кулонівських полів позитивного і від’ємного точкових зарядів зображено на
мал. 2. Так як електростатичне поле, яке створене будь-якою системою
зарядів, можна представити як суперпозицію кулонівських полів точкових зарядів,
зображених на рис. 2. Поля зображені на даному малюнку можна розглядати як
елементарні структурні одиниці («цеглинки») будь-якого електростатичного поля.
 |
| Мал.2 Силові лінії поля точкового заряду. |
Як приклад
застосування принципу суперпозиції полів розгляньмо поле електричного диполя.
Електричний диполь – це система двох
однакових по модулю зарядів різного знака q і –q, росташованих на деякій
віддалі l. На мал. 3 зображено
картину силових ліній дипольного поля.
Важливою
характеристикою електричного диполя є так званий дипольний момент р:
р = lq,
де l –
вектор, направлений від від’ємного заряду до додатнього.
Диполь
може слугувати електричною моделлю багатьох молекул.
Електричним
дипольним моментом володіє, наприклад, нейтральна молекула води (H2O),
так як центри двох атомів водню розташовані не на одній прямі з центром атома
кисню, а під кутом 105° (мал. 4). Дипольний момент молекули води
p = 6,2·10–30 Кл · м.
В
багатьох задачах електростатики потрібно за заданим разподілом зарядів
визначити електричне поле Е. Нехай, наприклад, потрібно знайти електричне поле
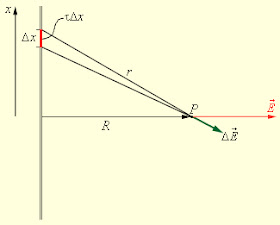
довгої однорідно зарядженої нитки (мал. 5) на віддалі R від неї.
Поле
в точці спостереження P можна представити як суперпозицію кулонівських полів,
які створюють малі елементи Δx нитки, з зарядом τΔx, де τ – заряд
нитки на одиницю довжини. Задача зводиться до сумування (інтегрування)
елементарних полів ΔЕ. Результуюче поле
дорівнює:
Е = τ/2πε0∙R.
Вектор
Е всюди напрямлений вздовж радіуса
R. Це випливає з симетрії задачі. Вже
цей простий приклад показує, що прямий шлях визначення поля за заданим
розподілом зарядів приводить до громіздких математичних розрахунків. В деяких
випадках можна значно спростити розрахунки, якщо скористатись теоремою Гауса,
яка виражає фундаментальні властивості електричного поля.
Жирнішим виділено вектори
Доцільно прочитати:
- 1. Електричний заряд.
- 2. Закон Кулона.
- 3. Вимірювання ЕРС джерела.
- 4. ККД електричної схеми.
- 5. Закон Ома для електролітів.
- 6. Закон Ома.