Комплексні числа
У багатьох розділах математики та її застосуваннях неможливо
обмежитись розглядом лише дійсних чисел.
Вже досить давно під час розв’язування різних задач виникла потреба добувати
квадратний корінь з від’ємних чисел.
Щоб ця дія стала можливою, ввели множину нових чисел.
Означення комплексного числа і уявної одиниці
Числоa+bi , деa іb — будь-які дійсні числа,i — уявна одиниця, називається комплексним числом (a — дійсна частина,bi — уявна частина комплексного числа, аb — коефіцієнт при уявній частині).
Число, квадрат якого дорівнює−1 , позначають буквоюi і називають уявною одиницею (i — перша буква латинського слова imaginarius — уявний).
Тобто, для символу
Записa+bi називають алгебраїчною формою комплексного числа.
Примітка! Слово «комплексний» означає складений.
Часто комплексне число позначають буквою Множина дійсних чисел є частиною (підмножиною) множини комплексних чисел.
Для комплексних чисел означені алгебраїчні операції додавання та множення, які узагальнюють додавання та множення дійсних чисел із зберіганням властивостей асоціативності, комутативності та дистрибутивності.
Які комплексні числа називаються рівними, спряженими, протилежними?
Два комплексних числаa+bi іc+di рівні між собою тоді і тільки тоді, колиa=c іb=d , тобто, коли рівні їх дійсні частини і коефіцієнти при уявних частинах.
Поняття «більше» і «менше» для комплексних чисел не має сенсу.
Ці числа за величиною не порівнюють.
Тому не можна, наприклад, сказати, яке з двох комплексних чисел більше
Числаa+bi іa−bi , дійсні частини яких рівні, а коефіцієнти при уявних частинах рівні за модулем, але протилежні за знаком, називають спряженими.
Приклади.
- Спряженими є комплексні числа
4+3i та4−3i . - Якщо дано число
6i , то спряженим до нього є−6i . - До числа
11 спряженим буде11 , бо11+0i=11−0i .
Числаa+bi і−a−bi називаються протилежними. Тобто, два числаa+bi та−a−bi , сума яких дорівнює нулю, називають протилежними.
Дії над комплексними числами.
Нехай дано два комплексні числаа) Додавання комплексних чисел
Сумою двох комплексних чиселa1+b1i іa2+b2i називається комплексне число(a1+a2)+(b1+b2)i , дійсна частина якого і коефіцієнт при уявній частині дорівнюють відповідно сумі дійсних частин і коефіцієнтів при уявних частинах додатків.
Приклади (додавання комплексних чисел):
(−3+5i)+(4−8i)=(−3+4)+(5−8)i=1−3i (3+2i)+(−1−5i)=(3−1)+(2−5)i=2−3i (2+3i)+(6−3i)=(2+6)+(3−3)i=8−0i=8 (10−3i)+(−10+3i)=(10−10)+(−3+3)i=0−0i=0
Примітка! Означення суми комплексних чисел поширюється і на випадок трьох і більше доданків.
б) Віднімання комплексних чисел
Різницею двох комплексних чиселa1+b1i іa2+b2i називається комплексне число(a1−a2)+(b1−b2)i .
Приклади (віднімання комплексних чисел):
(−5+2i)−(3−5i)=(−5−3)+(2−(−5))i=−8+7i (6+7i)−(6−5i)=(6−6)+(7+5)i=12i (0,3+2,5i)−(−0,75+1,5i)=
=(0,3+0,75)+(2,5−1,5)i=1,05+i
в) Множення комплексних чисел
Добутком двох комплексних чиселa1+b1i іa2+b2i називається комплексне число(a1a2−b1b2)+(a1b2+b1a2)i .
Приклад (множення комплексних чисел):
Добуток двох спряжених комплексних чисел:
г) Ділення комплексних чисел.
Часткою комплексних чиселa1+b1i іa2+b2i називається комплексне число
Приклад (знайти частку комплексних чисел):
Геометричне зображення комплексного числа
Комплексне числоz=a+bi геометрично зображують точкоюM(a;b) координатної площини.
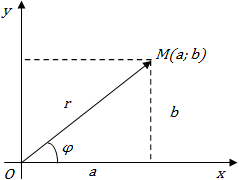 |
| Геометричне зображення комплексного числа. |
Довжина вектора, який зображає комплексне число, називається модулем цього комплексного числа. Модуль комплексного числа позначаєтьсяr . Тобто
Кутφ між додатним напрямком осі абсцис і векторомOM→ називається аргументом комплексного числа.
Примітка! Кожне комплексне число, що не дорівнює нулю, має нескінчену множину аргументів,
які відрізняються один від одного на 360∘k , де k∈Z .
Тригонометрична форма комплексного числа.
ВиразившиПрава частина цієї тотожності називається тригонометричною формою комплексного числа.
Дії над комплексними числами, які записані у тригонометричній формі
Нехай задано два комплексні числа:-
Множення
z1⋅z2=r1⋅r2(cos(φ1+φ2)+isin(φ1+φ2)). -
Ділення
z1z2=r1r2(cos(φ1−φ2)+isin(φ1−φ2)). -
Піднесення до степеня (формула Муавра)
zn=rn(cosnφ+isinnφ). -
Добування кореня
z√n=r(cosφ+isinφ)−−−−−−−−−−−−−√n= =r√n(cosφ+2πkn+isinφ+2πkn), k=0,1,2,...,n−1.